Opzoeklijsten, grafieken, statistieken en draaitabellen

Nadat we de basisfuncties, celverwijzingen en datum- en tijdfuncties hebben besproken, duiken we nu in enkele van de meer geavanceerde functies van Microsoft Excel. We presenteren methoden om klassieke problemen op te lossen in financiën, verkooprapporten, verzendkosten en statistieken.

SCHOOLNAVIGATIE

1. Waarom heeft u formules en functies nodig??
2. Een formule definiëren en maken
3. Relatieve en absolute celverwijzing en opmaak
4. Handige functies die u moet leren kennen
5. Opzoeklijsten, grafieken, statistieken en draaitabellen

Deze functies zijn belangrijk voor bedrijven, studenten en mensen die gewoon meer willen leren.

VLOOKUP en HLOOKUP

Hier is een voorbeeld om de functies voor verticale opzoek (VLOOKUP) en horizontale opzoek (HLOOKUP) te illustreren. Deze functies worden gebruikt om een ​​getal of andere waarde te vertalen naar iets dat begrijpelijk is. U kunt bijvoorbeeld VERT.ZOEKEN gebruiken om een ​​onderdeelnummer te nemen en de artikelbeschrijving terug te sturen.

Om dit te onderzoeken, gaan we terug naar onze spreadsheet "Decision Maker" in deel 4, waarin Jane probeert te beslissen wat hij of zij naar school moet dragen. Ze is niet langer geïnteresseerd in wat ze draagt, omdat ze een nieuw vriendje heeft neergezet, dus ze zal nu willekeurige outfits en schoenen dragen.

In de spreadsheet van Jane somt ze outfits op in verticale kolommen en schoenen, horizontale kolommen.

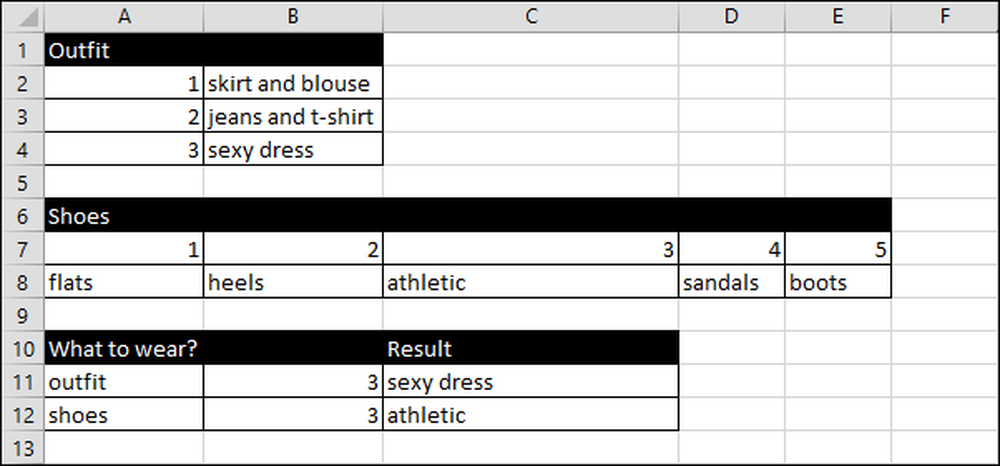
Ze opent de spreadsheet en de functie RANDBETWEEN (1,3) genereert een getal tussen of gelijk aan één en drie voor de drie soorten outfits die ze kan dragen.

Ze gebruikt de functie RANDBETWEEN (1,5) om uit vijf soorten schoenen te kiezen.

Aangezien Jane geen nummer kan dragen, moeten we dit naar een naam converteren, dus we gebruiken zoekfuncties.

We gebruiken de VERT.ZOEKEN-functie om het outfitnummer naar de outfitnaam te vertalen. HLOOKUP vertaalt van schoennummer naar de verschillende soorten schoenen in de rij.

De spreadsheet werkt als volgt voor outfits:

Excel kiest een willekeurig getal van één tot drie, omdat ze drie outfitopties heeft.

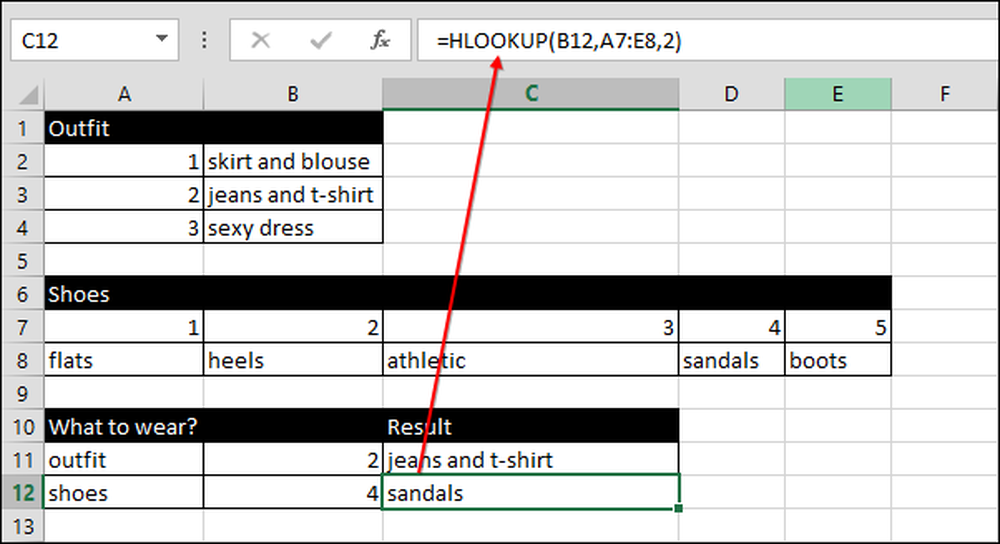
Vervolgens vertaalt de formule het getal naar tekst met = VLOOKUP (B11, A2: B4,2), waarbij willekeurig getal de waarde uit B11 gebruikt om in het bereik A2: B4 te zoeken. Vervolgens wordt het resultaat (C11) weergegeven uit de gegevens in de tweede kolom.

We gebruiken dezelfde techniek om schoenen te selecteren, maar deze keer gebruiken we VOOKUP in plaats van HORIZ.ZOEKEN.

Voorbeeld: basisstatistieken

Bijna iedereen kent één formule uit statistieken - gemiddeld - maar er is nog een statistiek die belangrijk is voor het bedrijfsleven: standaardafwijking.

Bijvoorbeeld, velen van hen die naar de universiteit zijn gegaan, hebben zich zorgen gemaakt over hun GEZETEN score. Ze willen misschien weten hoe ze rangschikken in vergelijking met andere studenten. Universiteiten willen dit ook weten, omdat veel universiteiten, vooral prestigieuze universiteiten, studenten met lage SAT-scores afwijzen.

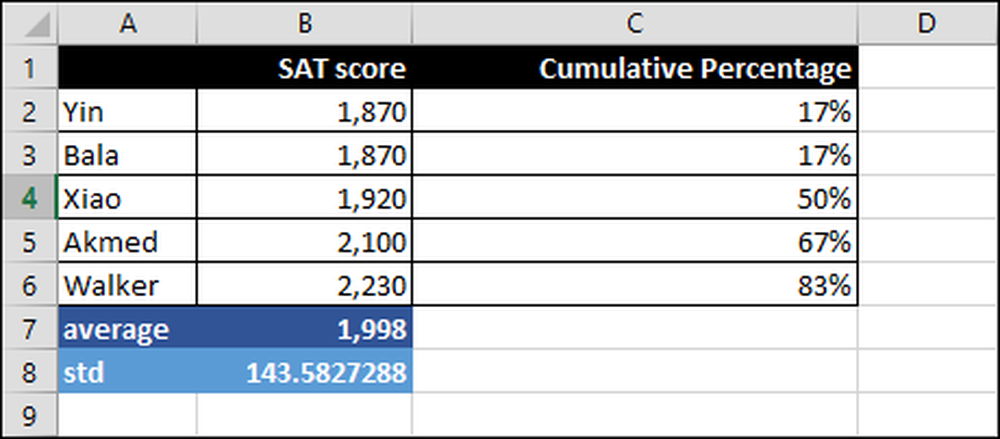
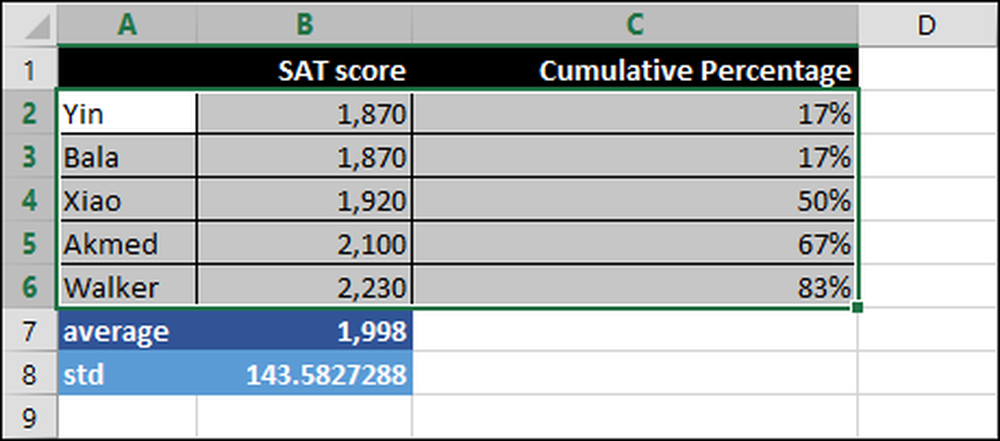
Dus hoe zouden wij, of een universiteit, SAT-scores meten en interpreteren? Hieronder zijn SAT scores voor vijf studenten, variërend van 1.870 tot 2.230.

De belangrijkste te begrijpen cijfers zijn:

Gemiddelde - Gemiddeld wordt ook wel het 'gemiddelde' genoemd.

Standaarddeviatie (STD of σ) - Dit getal geeft aan hoe wijdverspreid een reeks getallen is. Als de standaarddeviatie groot is, liggen de getallen ver uit elkaar en als deze nul is, zijn alle getallen hetzelfde. Je zou kunnen zeggen dat de standaardafwijking het gemiddelde verschil is tussen de gemiddelde waarde en de waargenomen waarde, namelijk 1.988 en elke SAT-score. Houd er rekening mee dat het gebruikelijk is om de standaarddeviatie af te korten met het Griekse symbool sigma "σ."

Percentiel Rank - Wanneer een student een hoge score krijgt, kunnen ze opscheppen dat ze in het bovenste 99 percentiel zitten of zoiets. "Percentielrang" betekent dat het percentage scores lager is dan een bepaalde score.

Standaarddeviatie en waarschijnlijkheid zijn nauw met elkaar verbonden. Je kunt zeggen dat voor elke standaardafwijking de waarschijnlijkheid of waarschijnlijkheid dat dat aantal zich binnen dat aantal standaarddeviaties bevindt:

soa	Percentage scores	Bereik van SAT-scores
1	68%	1,854-2,142
2	95%	1,711-2,285
3	99,73%	1,567-2,429
4	99,994%	1,424-2,572

Zoals je kunt zien, is de kans dat een GEZETEN score buiten 3 SOA's ligt vrijwel nul, omdat 99,73 procent van de scores binnen 3 SOA's valt.

Laten we nu de spreadsheet opnieuw bekijken en uitleggen hoe het werkt.

Nu leggen we de formules uit:

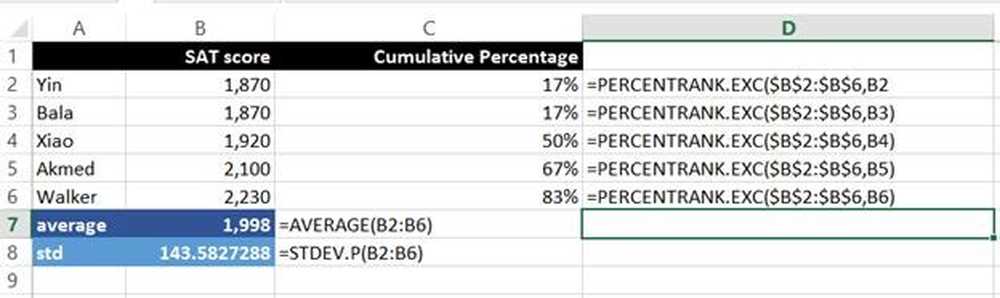
= GEMIDDELDE (B2: B6)

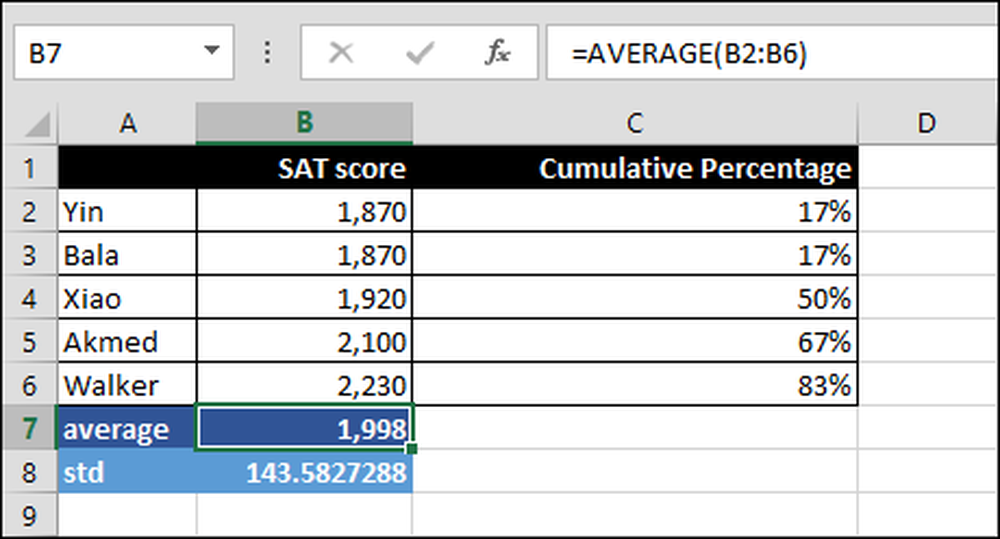
Het gemiddelde van alle scores over het bereik B2: B6. Concreet is de som van alle scores gedeeld door het aantal mensen dat de test heeft afgelegd.

= STDEV.P (B2: B6)

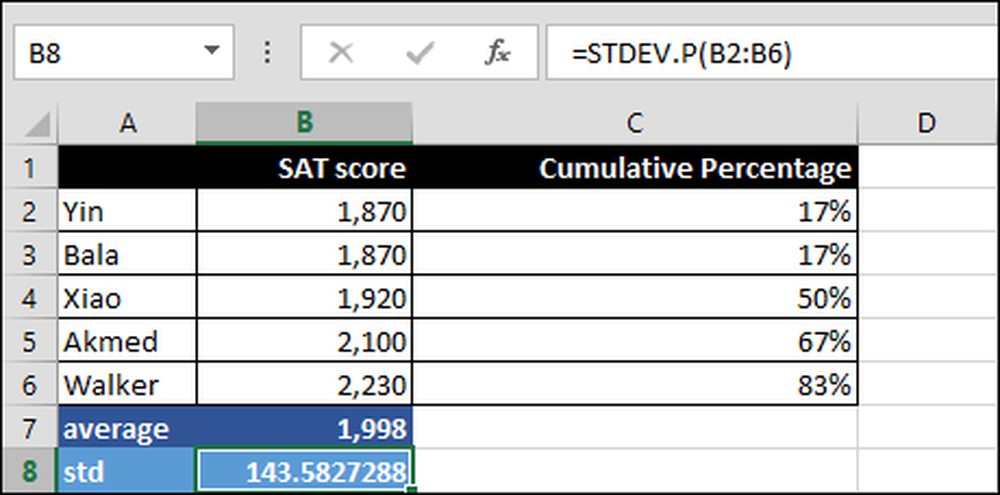
De standaardafwijking over het bereik B2: B6. De ".P" betekent dat STDEV.P wordt gebruikt voor alle scores, d.w.z. de gehele populatie en niet slechts een subset.

= PERCENTRANK.EXC ($ B $ 2: $ B $ 6, B2)

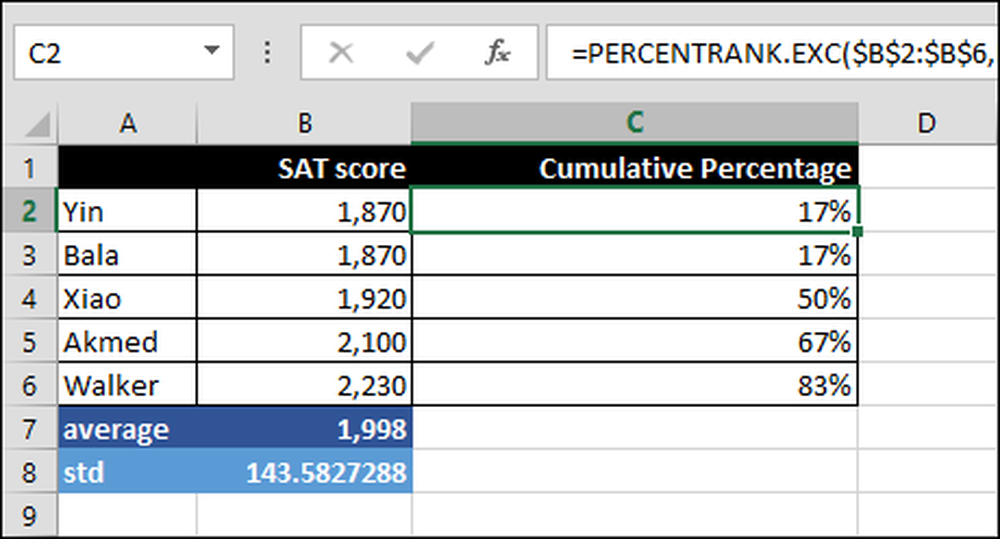
Dit berekent het cumulatieve percentage over het bereik B2: B6 op basis van de SAT-score, in dit geval B2. 83 procent van de scores ligt bijvoorbeeld onder de score van Walker.

Grafische weergave van de resultaten

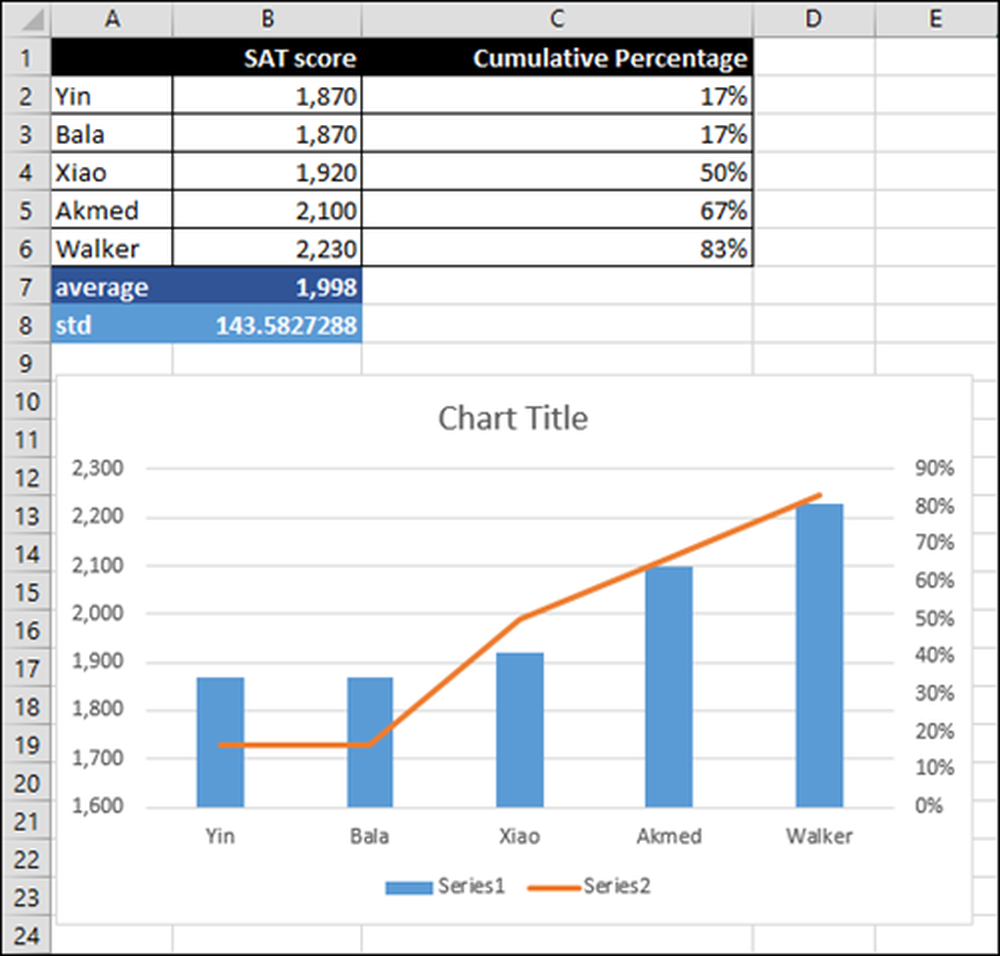
Door de resultaten in een grafiek te plaatsen, is het gemakkelijker om de resultaten te begrijpen, plus kunt u het in een presentatie laten zien om uw punt duidelijker te maken.

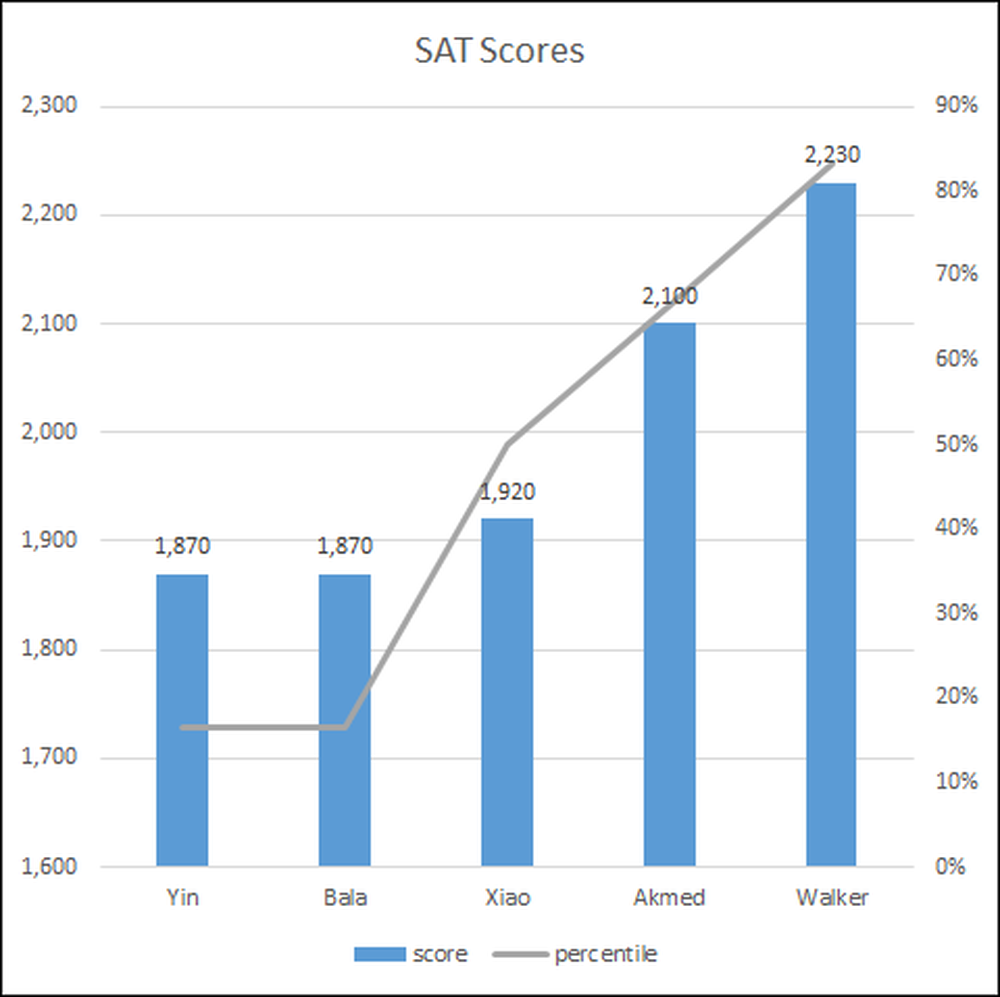
De studenten staan ​​op de horizontale as en hun SAT-scores worden weergegeven als een blauwe staafdiagram op een schaal (verticale as) van 1.600 tot 2.300.

De percentielrangschikking is de rechter verticale as van 0 tot 90 procent en wordt weergegeven door de grijze lijn.

Hoe een diagram te maken

Het maken van een diagram is een onderwerp op zich, maar we zullen in het kort uitleggen hoe de bovenstaande grafiek is gemaakt.

Selecteer eerst het cellenbereik dat in de grafiek moet voorkomen. In dit geval A2 tot C6 omdat we zowel de nummers als de namen van de studenten willen.

Selecteer "Grafieken" -> "Aanbevolen kaarten" in het menu "Invoegen":

De computer beveelt een diagram met de "Geclusterde kolom, secundaire as" aan. Het deel "secundaire as" betekent dat het twee verticale assen tekent. In dit geval is deze grafiek degene die we willen hebben. We hoeven niets anders te doen.

U kunt de kaart verplaatsen en de grootte ervan aanpassen totdat u deze hebt zoals de maat en de positie die u wilt. Als u tevreden bent, kunt u het diagram opslaan in de spreadsheet.

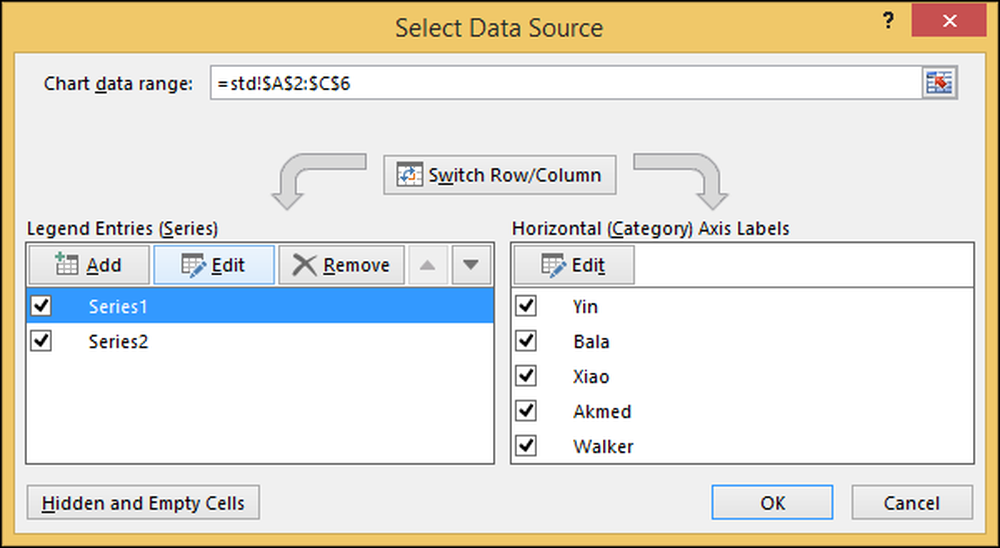
Als u met de rechtermuisknop op het diagram klikt en vervolgens op 'Gegevens selecteren', wordt weergegeven welke gegevens voor het bereik zijn geselecteerd.

De "Aanbevolen grafieken" -functie beschermt u gewoonlijk tegen ingewikkelde details, zoals bepalen welke gegevens moeten worden opgenomen, hoe labels moeten worden toegewezen en hoe de linker- en rechter verticale assen moeten worden toegewezen..

Klik in het dialoogvenster "Gegevensbron selecteren" op "score" onder "Legend Entries (Series)" en druk op "Bewerken" en wijzig dit in "Score".

Wijzig vervolgens reeks 2 ("percentiel") in "Percentiel".

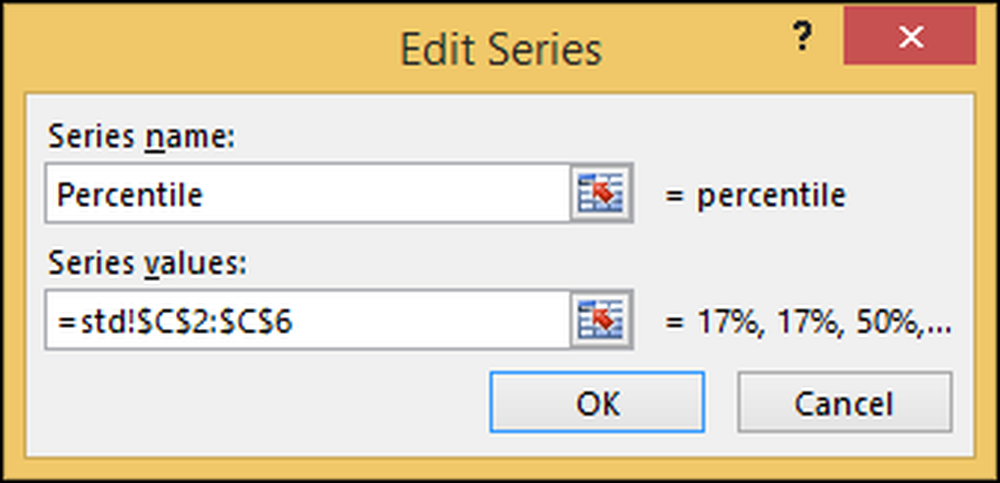
Keer terug naar uw grafiek en klik op de "Grafiektitel" en verander het naar "SAT Scores." Nu hebben we een volledige grafiek. Het heeft twee horizontale assen: één voor SAT score (blauw) en één voor cumulatief percentage (oranje).

Voorbeeld: het transportprobleem

Het transportprobleem is een klassiek voorbeeld van een type wiskunde dat 'lineaire programmering' wordt genoemd. Hiermee kunt u een waarde maximaliseren of minimaliseren die onderhevig is aan bepaalde beperkingen. Het heeft veel toepassingen voor een breed scala aan zakelijke problemen, dus het is handig om te leren hoe het werkt.

Voordat we aan dit voorbeeld beginnen, moeten we de "Excel Solver" inschakelen.

Schakel Oplosser-invoegtoepassing in

Selecteer "Bestand" -> "Opties" -> "Add-ins". Klik onder aan de invoegtoepassingen op de knop 'Start' naast 'Beheren: Excel-invoegtoepassingen'.

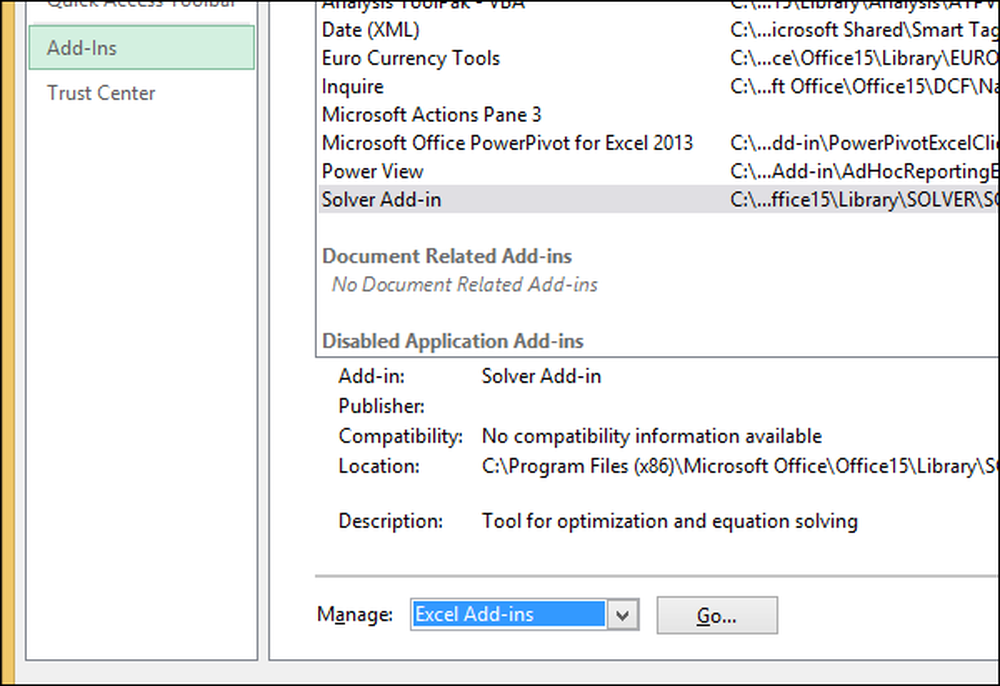
Klik in het menu dat verschijnt op het selectievakje om "Oplosser invoegtoepassing" in te schakelen en klik op "OK".

Voorbeeld: bereken de laagste iPad-verzendkosten

Stel dat we iPads verzenden en we proberen onze distributiecentra te vullen met de laagste transportkosten die mogelijk zijn. We hebben een overeenkomst gesloten met een trucking- en luchtvaartmaatschappij om iPads vanuit Shanghai, Beijing en Hong Kong naar de onderstaande distributiecentra te verzenden.

De prijs voor het verzenden van elke iPad is de afstand van de fabriek naar het distributiecentrum naar de fabriek gedeeld door 20.000 kilometer. Het is bijvoorbeeld 8.024 km van Shanghai naar Melbourne, dat is 8.024 / 20.000 of $ .40 per iPad.

De vraag is hoe we al deze iPads van deze drie fabrieken naar deze vier bestemmingen verzenden tegen de laagst mogelijke kosten?

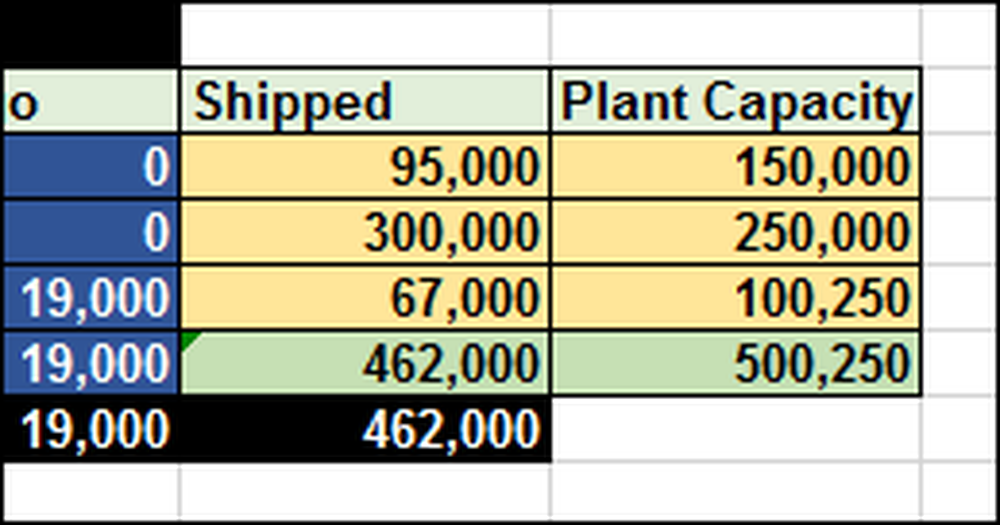
Zoals je je kunt voorstellen, zou het uitzoeken van dit heel moeilijk kunnen zijn zonder een formule en tool. In dit geval moeten we 462.000 (F12) totale iPads verzenden. De installaties hebben een beperkte capaciteit van 500.250 (G12) -eenheden.

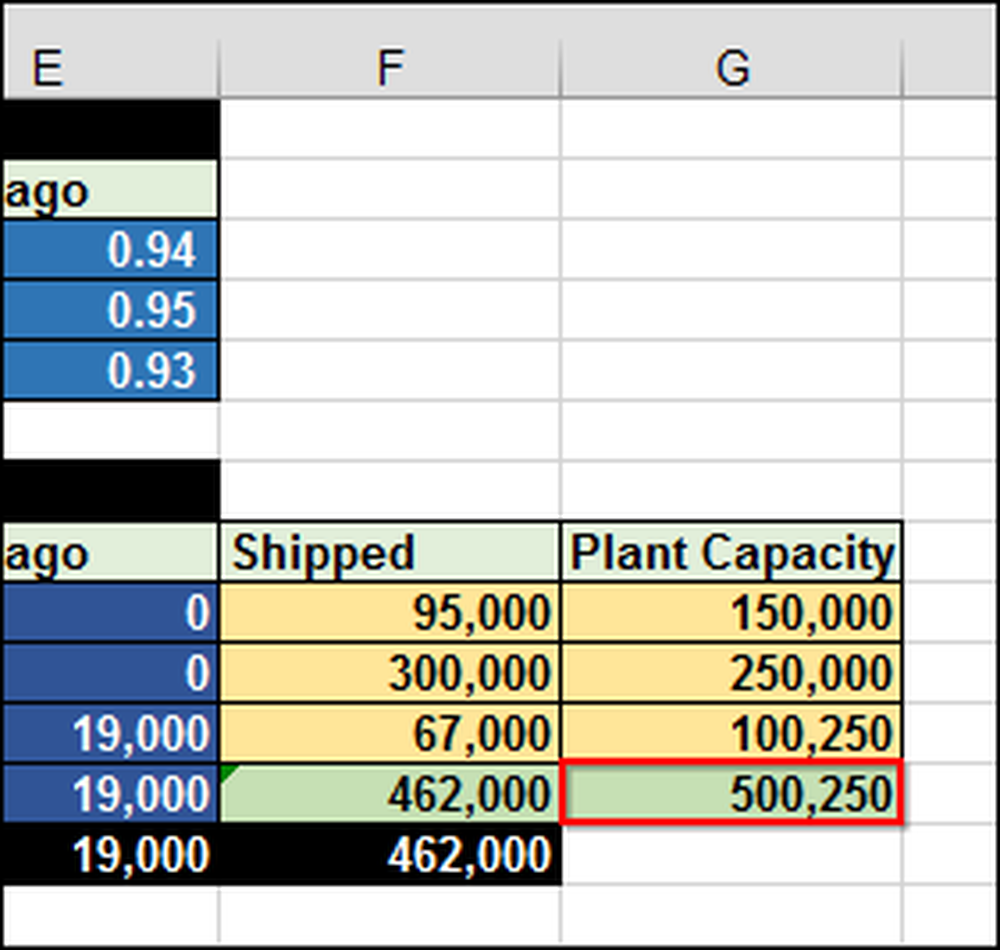
In de spreadsheet, zodat u kunt zien hoe het werkt, hebben we 1 ingetypt in cel B10, wat betekent dat we 1 iPad van Shanghai naar Melbourne willen verzenden. Aangezien de transportkosten langs die route $ 0,40 per iPad bedragen, bedragen de totale kosten (B17) $ 0,40.

Het aantal is berekend met behulp van de functie = SOMPRODUCT (kosten, verzonden) "kosten" zijn de bereiken B3: E5.

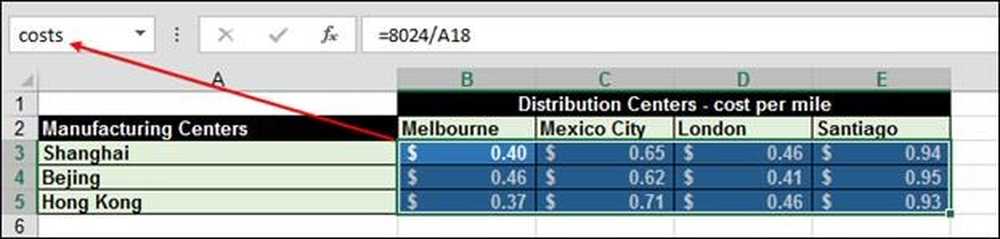
En "verzonden" zijn het bereik B9: E11:

SUMPRODUCT vermenigvuldigt "kosten" maal het bereik "verzonden" (B14). Dat wordt 'matrixvermenigvuldiging' genoemd.

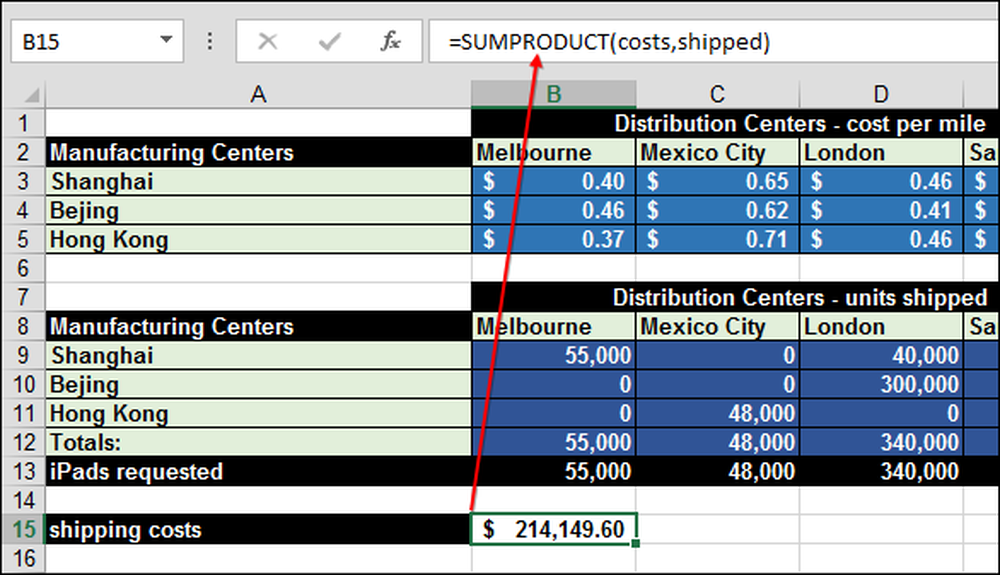
Om SUMPRODUCT correct te laten werken, moeten de twee matrices - kosten en verzonden - dezelfde grootte hebben. U kunt deze beperking omzeilen door extra kosten te maken en kolommen en rijen met nulwaarde te verzenden zodat de matrices dezelfde grootte hebben en er geen invloed op de totale kosten is.

De Oplosser gebruiken

Als alles wat we moesten doen was vermenigvuldigen de matrices "kosten" tijden "verzonden" dat zou niet al te ingewikkeld zijn, maar we hebben ook te maken met beperkingen daar.

We moeten verzenden wat elk distributiecentrum vereist. We zetten dat constant in de solver zoals deze: $ B $ 12: $ E $ 12> = $ B $ 13: $ E $ 13. Dit betekent dat de som van wat wordt verzonden, d.w.z. de totalen in cellen $ B $ 12: $ E $ 12, moet groter zijn dan of gelijk aan wat elk distributiecentrum vereist ($ B $ 13: $ E $ 13).

We kunnen niet meer verzenden dan we produceren. We schrijven die beperkingen als volgt: $ F $ 9: $ F $ 11 <= $G$9:$G$11. Put another way, what we ship from each plant $F$9:$F$11 cannot exceed (must be less than or equal to) the capacity of each plant: $G$9:$G$11.

Ga nu naar het menu "Gegevens" en druk op de knop "Oplosser". Als de knop "Oplosser" er niet is, moet u de invoegtoepassing Oplosser inschakelen.

Voer de twee eerder gedetailleerde voorwaarden in en selecteer het bereik "Verzendingen", het bereik van getallen die we met Excel willen berekenen. Kies ook het standaardalgoritme "Simplex LP" en geef aan dat we cel B15 ("totale verzendkosten") willen "minimaliseren", waar staat "Doelstelling instellen".

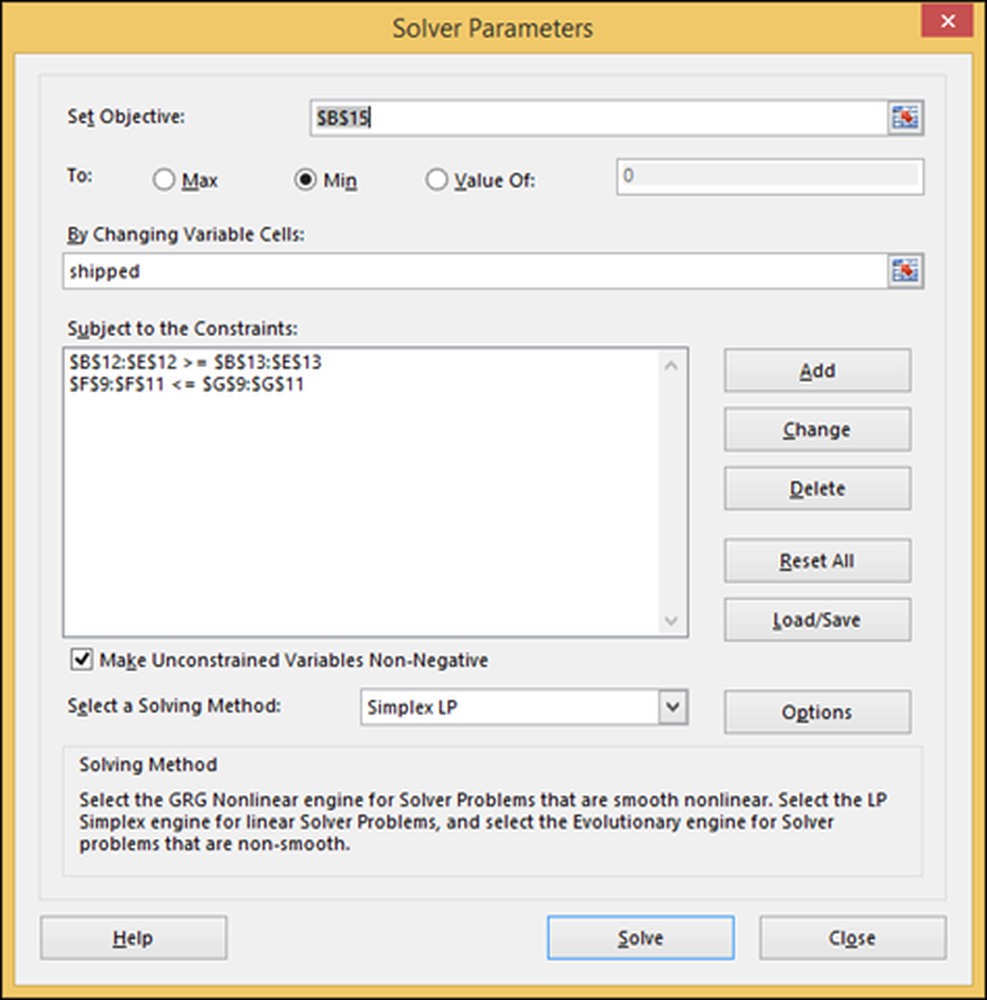
Druk op "Oplossen" en Excel slaat de resultaten op in de spreadsheet, wat we willen. Je kunt dit ook opslaan, zodat je kunt spelen met andere scenario's.

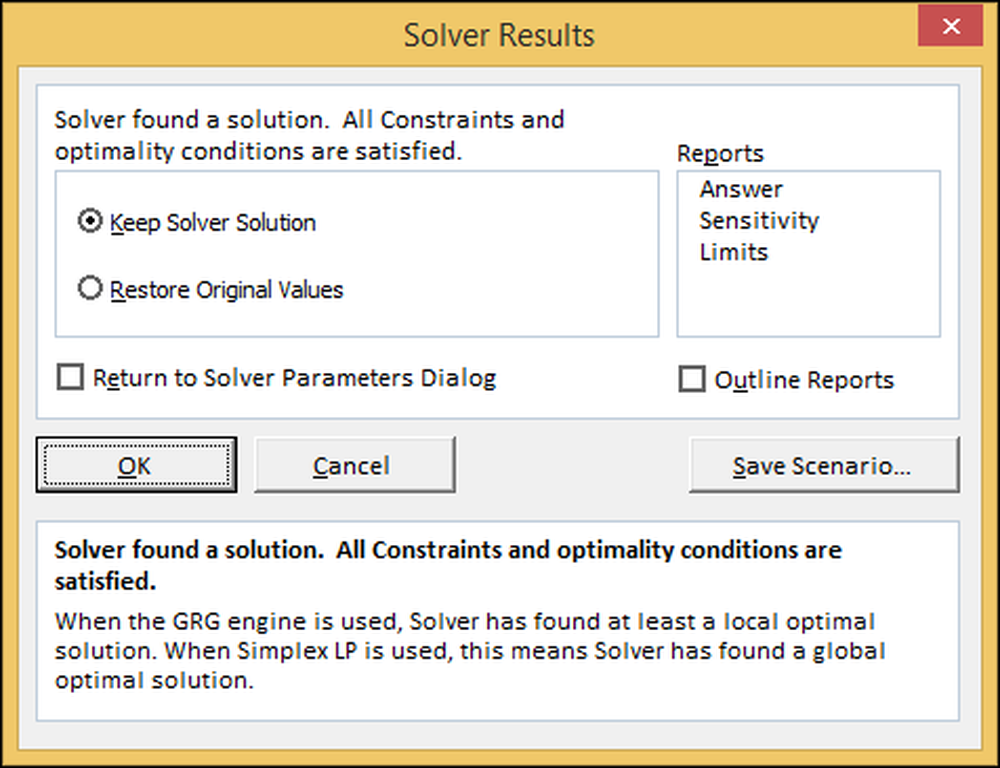
Als de computer zegt dat het geen oplossing kan vinden, dan heb je iets gedaan dat niet logisch is, je hebt bijvoorbeeld misschien meer iPads gevraagd dan de planten kunnen produceren.

Hier zegt Excel dat het een oplossing heeft gevonden. Druk op "OK" om de oplossing te behouden en terug te keren naar de spreadsheet.

Voorbeeld: netto huidige waarde

Hoe beslist een bedrijf of hij in een nieuw project wil investeren? Als de "netto contante waarde" (NPV) positief is, zullen ze erin investeren. Dit is een standaardaanpak van de meeste financiële analisten.

Stel dat het mijnbedrijf Codelco de kopermijn van Andinas wil uitbreiden. De standaardbenadering om te bepalen of een project wordt uitgevoerd, is om de netto contante waarde te berekenen. Als de NPV groter is dan nul, dan is het project winstgevend gezien twee inputs (1) tijd en (2) kapitaalkosten.

In gewoon Engels betekent de kapitaalkosten hoeveel dat geld zou verdienen als ze het gewoon bij de bank achterlaten. U gebruikt de kapitaalkosten om contante waarden als contante waarde te presenteren, met andere woorden $ 100 in vijf jaar kan vandaag $ 80 zijn.

In het eerste jaar wordt $ 45 miljoen gereserveerd als kapitaal om het project te financieren. De accountants hebben vastgesteld dat hun kapitaalkosten zes procent zijn.

Terwijl ze beginnen te mijnen, begint het geld binnen te komen als het bedrijf het koper dat ze produceren vindt en verkoopt. Het is duidelijk dat hoe meer ze mijnen, hoe meer geld ze verdienen, en hun voorspelling laat zien dat hun cashflow toeneemt tot ze $ 9 miljoen per jaar bereikt.

Na 13 jaar is de NPV $ 3.945.074 USD, dus het project zal winstgevend zijn. Volgens financiële analisten is de "terugbetalingsperiode" 13 jaar.

Een draaitabel maken

Een "draaitabel" is eigenlijk een rapport. We noemen ze draaitabellen omdat u ze eenvoudig van het ene type rapport naar het andere kunt schakelen zonder een volledig nieuw rapport te hoeven maken. Dus zij spil op zijn plaats. Laten we een eenvoudig voorbeeld tonen dat de basisbegrippen leert.

Voorbeeld: verkooprapporten

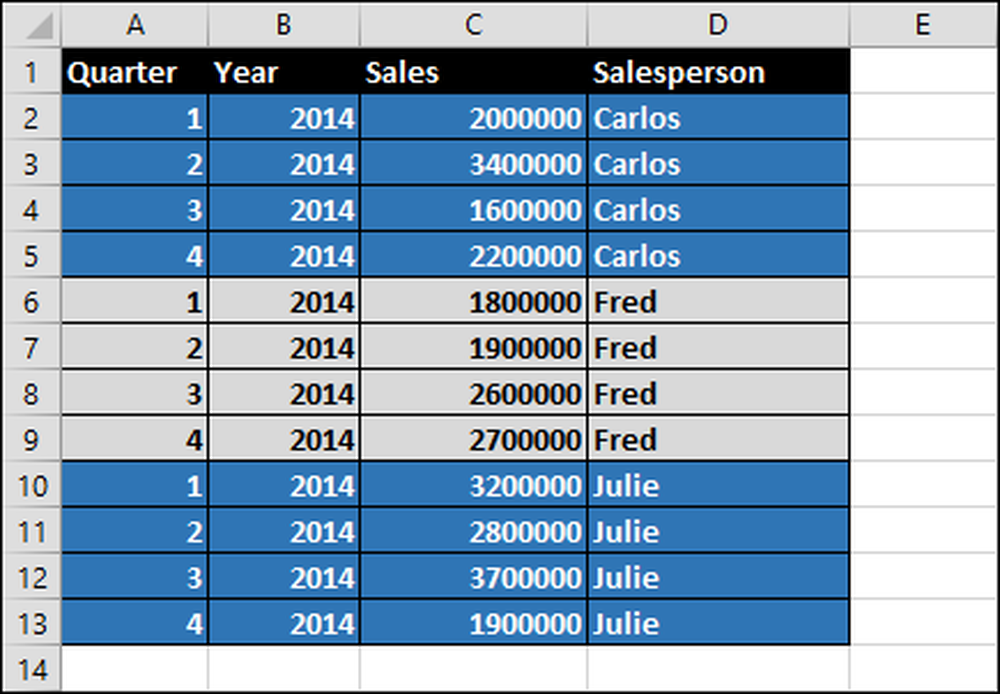
Verkopers zijn erg competitief (dat hoort erbij als verkoper), dus willen ze natuurlijk weten hoe ze tegen het einde van het kwartaal en het einde van het jaar tegen elkaar presteren, plus hoeveel hun commissies zullen zijn.

Stel dat we drie verkopers hebben - Carlos, Fred en Julie - die allemaal aardolie verkopen. Hun omzet in dollars per fiscaal kwartaal voor het jaar 2014 wordt weergegeven in het onderstaande spreadsheet.

Voor het genereren van deze rapporten maken we een draaitabel:

Selecteer "Insert -> Pivot Table", het staat aan de linkerkant van de werkbalk:

Selecteer alle rijen en kolommen (inclusief de naam van de verkoper) zoals hieronder getoond:

Het draaitabeldialoogvenster verschijnt aan de rechterkant van het werkblad.

Als we op alle vier de velden in het dialoogvenster met draaitabellen (kwartaal, jaar, verkoop en verkoper) klikken, voegt Excel een rapport aan de spreadsheet toe dat geen zin heeft, maar waarom?

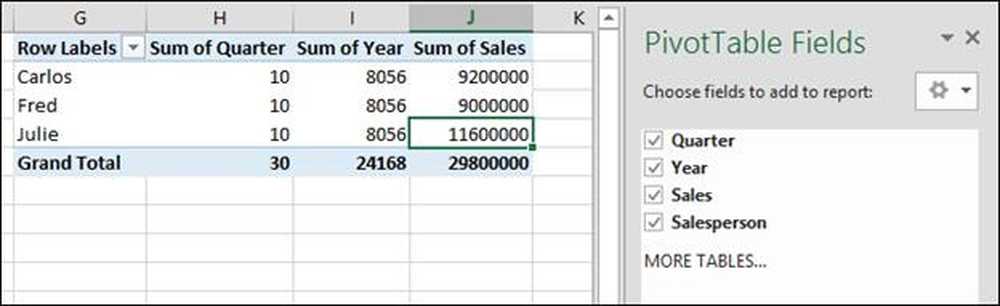
Zoals u kunt zien, hebben we alle vier de velden geselecteerd om aan het rapport toe te voegen. Het standaardgedrag van Excel bestaat uit het groeperen van rijen op tekstvelden en vervolgens het optellen van alle overige rijen.

Hier geeft het ons de som van het jaar 2014 + 2014 + 2014 + 2014 = 24.168, en dat is onzin. Het gaf ook de som van de kwartalen 1 + 2 + 3 + 4 = 10 * 3 = 3 0. We hebben deze informatie niet nodig, dus we deselecteren deze velden om ze van onze draaitabel te verwijderen.

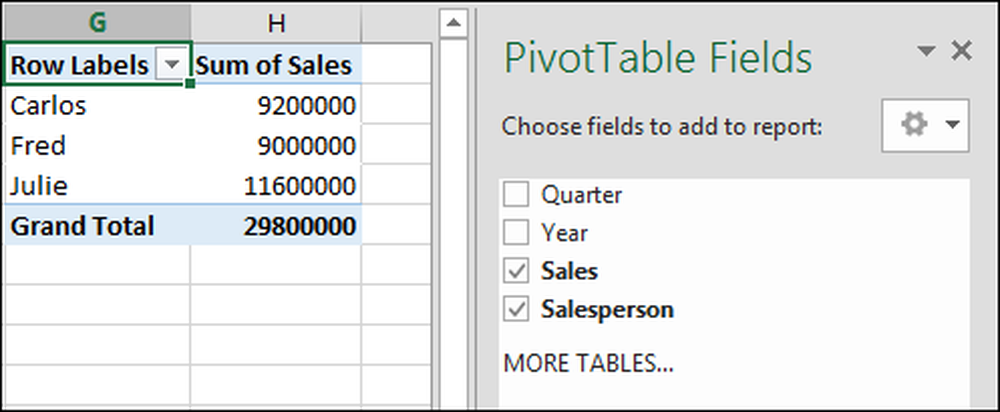
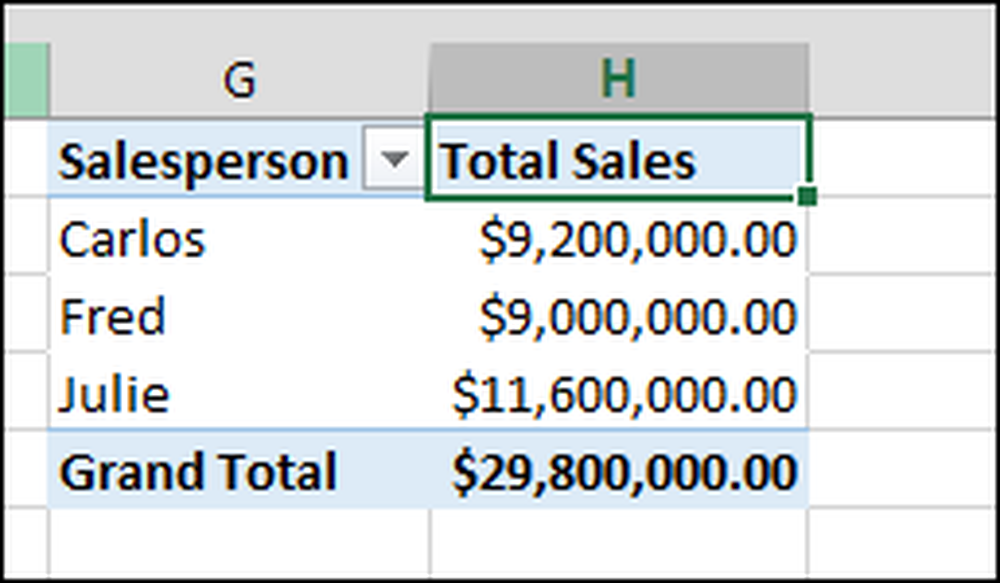
"Som van de omzet" (totale verkoop) is echter relevant, dus we zullen dit oplossen.

Voorbeeld: verkoop door verkoper

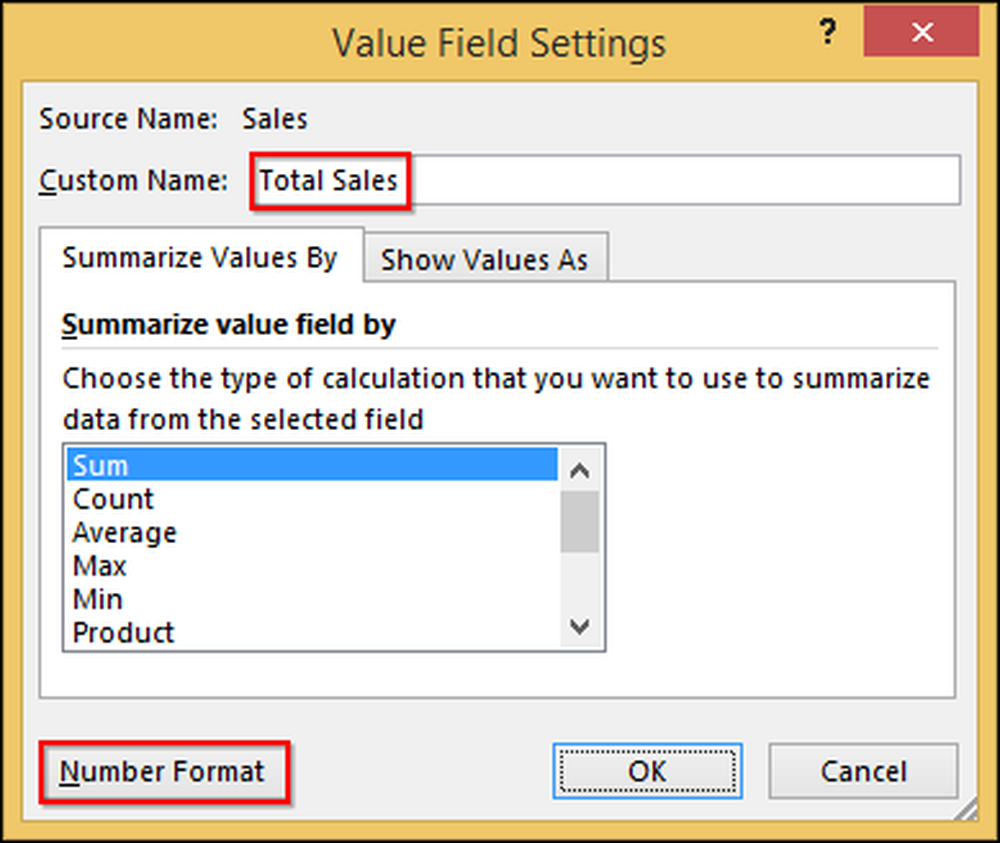
U kunt 'Som van verkopen' bewerken om 'Totale omzet' te zeggen, wat duidelijker is. U kunt de cellen ook opmaken als valuta, net zoals u andere cellen zou opmaken. Klik eerst op 'Som van verkopen' en selecteer 'Instellingen waardeveld'.

In het resulterende dialoogvenster veranderen we de naam in 'Totale omzet'. Klik vervolgens op 'Getalnotatie' en wijzig dit in 'Valuta'.

U kunt dan uw handwerk in de draaitabel bekijken:

Voorbeeld: verkopen door verkoper en kwartaal

Laten we nu subtotalen voor elk kwartaal toevoegen. Om subtotalen toe te voegen, klikt u met de linkermuisknop op het veld "Kwartaal" en houdt u het vast en sleept u het naar het gedeelte "rijen". U kunt het resultaat zien op de onderstaande screenshot:

Laten we, terwijl we bezig zijn, de waarden voor 'Sum of Quarter' verwijderen. Klik eenvoudig op de pijl en klik op "Veld verwijderen". In het screenshot ziet u nu dat we de rijen "Kwartier" hebben toegevoegd, die de omzet van elke verkoper per kwartaal opsplitst..

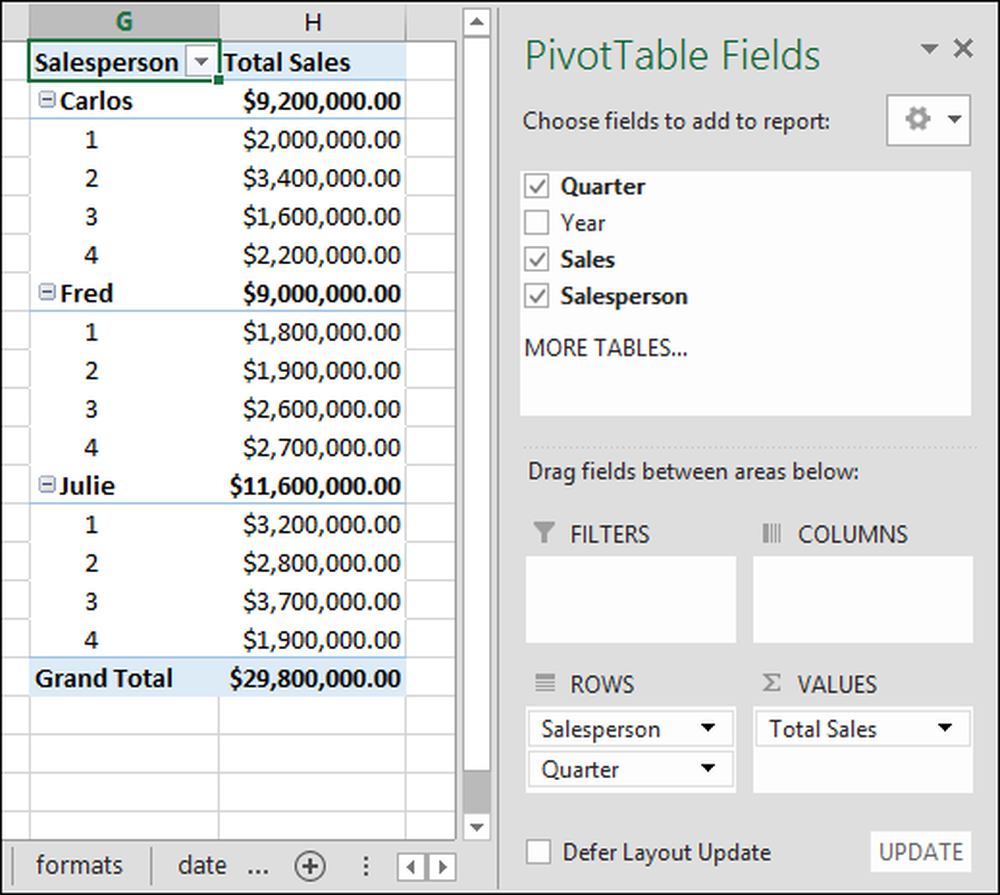
Met deze nieuwe vaardigheden in gedachten kunt u nu draaitabellen maken met uw eigen gegevens!

Conclusie

In afwachting hebben we enkele van de functies van de formules en functies van Microsoft Excel getoond waarmee u Microsoft Excel kunt toepassen op uw zakelijke, academische of andere behoeften.

Zoals je hebt gezien, is Microsoft Excel een enorm product met zoveel functies dat de meeste mensen, zelfs geavanceerde gebruikers, ze niet allemaal kennen. Sommige mensen zouden kunnen zeggen dat het ingewikkeld maakt; we voelen dat het uitgebreider is.

Hopelijk hebben we, door u veel voorbeelden uit de praktijk te presenteren, niet alleen de functies getoond die beschikbaar zijn in Microsoft Excel, maar hebben we u ook iets geleerd over statistiek, lineair programmeren, diagrammen maken, willekeurige getallen gebruiken en andere ideeën die u nu kunt gebruiken en gebruik op uw school of waar u werkt.

Onthoud dat als je terug wilt gaan en de les opnieuw wilt volgen, je vers kunt beginnen met les 1!